Pengertian Momen Inersia : Faktor, Penerapan, Contoh Soal Dan Rumusnya

Rumus, Contoh Soal, Penerapan, Faktor Dan Pengertian Momen Inersia

Momen Inersia Adalah besaran yang menyatakan ukuran kelembaman benda yang mengalami gerak rotasi. Momen inersia disebut juga dengan momen kelembaman. Data momen inersia suatu penampang dari struktur diharapkan pada perhitungan-perhitungan tegangan lentur, tegangan geser, tegangan torsi dan sebagainya .

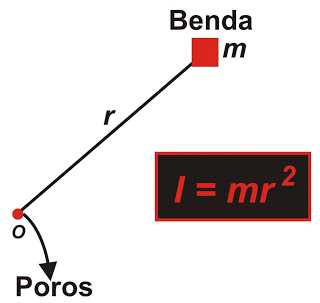
Adapun momen inersia yaitu suatu sifat kekakuan yang ditimbulkan perkalian luas dengan kuadrat jarak ke suatu garis lurus atau sumbu. Momen inersia dilambangkan dengan I.

Ada dua macam momen inersia yaitu
a. Momen Inersia linier yaitu momen inersia terhadap suatu garis lurus atau sumbu. Jika terhadap sumbu x yaitu Ix dan bila terhadap sumbu y yaitu Iy
b. Momen inersia polar yaitu momen inersia terhadap suatu titik perpotongan dua garis lurus atau sumbu. Dengan kata lain, bahwa inersia polar yaitu jumlah momen inersia linier terhadap sumbu x dan sumbu y . Momen inersia polar dilambangkan dengan Ip

Pada percobaan ini akan dibahas ihwal momen inersia suatu benda tegar dengan cara menguji korelasi antara momen gaya dengan percepatan sudut. Metode percobaan ini dengan melaksanakan percobaan sebanyak 3 kali dengan memakai variasi dari lempengan dan variasi massa beban yang digantungkan pada katrol.

pada percobaan tersebut diketahui korelasi antara momen gaya dan percepatan sudut. Dimana momen gaya mempunyai korelasi kesebandingan dengan percepatan sudutnya sehingga semakin besar percepatan sudutnya maka momen gayanya akan semakin besar dan sebaliknya. Dimana momen gaya merupakan hasil kali antara momen inersia dan percepatan sudut yang dilakukan benda tegar.

Dari hasil pengolahan data mampu diperoleh momen inersia pada tiga buah lempengan dengan jari-jari yang berbeda. diperoleh momen inersia dengan metode perhitungan matematis sebesar rumus innersia 2,39 x10-2 kgm2; 2,36 x 10-2 kgm2dan 2,341 x10-2 kgm2 ,dengan memakai percepatan gravitasi pada literatur yaitu 9,8 m/s2 diperoleh momen inersia sebesar 7,01 x10-3 kgm2; 5,72 x10-3 kgm2; dan 3,9×10-3 kgm2; dan dengan grafik diperoleh momen inersia sebesar 12,5 x 10-4kgm2 ; 7,35 x 10-4 kgm2; dan 2,82 x10-4 kgm2.

Konsep tersebut juga berlaku pada benda yang sedang berotasi, mirip halnya planet-planet di dalam tata surya mempunyai kecenderungan untuk tetap mempertahankan keadaan gerak rotasinya. Kecenderungan ini disebut momen inersia atau rotasi inersia. Hal ini mampu ditemukan dalam kehidupan sehari-hari.

Roda-roda sepeda yang berputar bekerjsama turut membantu pengendara biar sepeda tetap berdiri. Hal ini dikarenakan roda-roda sepeda itu cenderung tetap berputar pada bidang yang sama sehingga menciptakan sepeda lebih gampang untuk dikendarai.

Telah diketahui bahwa massa benda hanya bergantung pada jumlah kandungan zat di dalam benda. Perbedaannya dengan momen inersia yang selain bergantung pada kandungan zat di dalamnya atau massa benda, juga bergantung pada posisi massa tersebut ke sumbu putarnya. Semakin jauh posisi massa benda ke sentra rotasinya, semakin besar momen inersia benda tersebut.

Untuk lebih memahami ihwal momen inersia maka dilakukanlah praktikum kali ini yang bertujuan untuk mengetahui korelasi antara momen gaya dan percepatan sudut pada gerak melingkar, memilih besarnya nilai momen inersia dan membandingkannya dengan nilai yang terprediksi, serta mengetahui korelasi Inew (momen inersia benda terbebani) dengan I0 (momen inersia mula-mula).

TINJAUAN PUSTAKA
Momen inersia merupakan sifat kelembaman suatu benda yang berotasi atau dirotasikan terhadap sumbu tertentu. Momen inersia dinyatakan dengan simbol I, merupakan suatu besaran yang memperlihatkan perjuangan dari suatu sistem benda untuk menentang gerak rotasinya. Momen inersia juga menawarkan kecenderungan suatu sistem benda untuk terus berputar atau membisu sebagai reaksi terhadap gaya torsi dari luar. Jika suatu benda yang bebas berputar terhadap sebuah sumbu sulit untuk dibentuk berputar, maka momen inersianya terhadap sumbu itu besar [1]

Ketika sudut benda tegar mengalami percepatan, berarti benda tersebut mempunyai percepatan sudut. Jika ω1 dan ω2 merupakan kecepatan sudut pada waktu t1 dan t2, percepatan sudut rata-rata α11 mampu dihitung:
(1)
Percepatan sudut sesaat α ialah limit α11 pada ketika ∆t mendekati 0
(definisi percepatan sudut) (2)
Satuan percepatan sudut α ialah rad/sekon.[2]
Didefinisikan bahwa besarnya torsi yang terkait oleh gaya F oleh persamaan
(3)
dimana r merupakan jarak antara titik sentra dan titik yang diberi F, serta d ialah jarak tegak lurus dari titik sentra ke garis arah F. Besaran d disebut lengan momen (lengan pengungkit) dari F[5].
Gaya tangensial menghasilkan percepatan tangensial at dan
(4)
Besar torsi terhadap sentra bulat yang diakibatkan oleh gaya Ft adalah
(5)
Karena percepatan tangensial berafiliasi dengan percepatan sudut dengan persamaan sehingga besarnya torsi menjadi
Contoh Soal Momen Inersia

Artinya torsi yang bekerja pada partikel sebanding dengan percepatan sudutnya[2].
ialah momen inersia partikel bermassa m, yang berotasi sejauh r dari sumbu rotasi. persamaan ini juga menyatakan korelasi antara torsi, momen inersia dan percepatan sudut partikel yang melaksanakan gerak rotasi. Istilah kerennya, ini ialah persamaan Hukum II Newton untuk partikel yang berotasi.

Dari aturan II Newton kita ketahui bahwa: (7)
Torsi berafiliasi dengan gaya yang bekerja terhadap sentra dan dinyatakan dengan

Walaupun setiap elemen massa mempunyai percepatan linier at yang berbeda, semua mempunyai percepatan sudut yang sama. Dengan ini kita mampu mengintegralkan persamaan diatas untuk menerima jumlah torsi pada O alasannya ialah gaya luar :

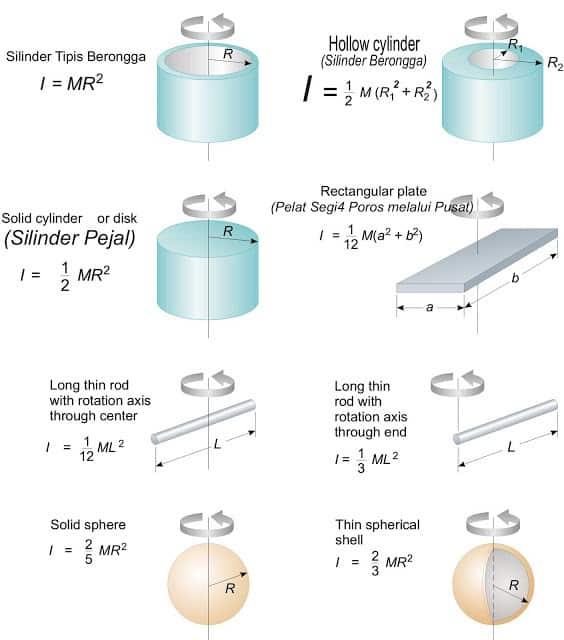
Momen inersia pada benda kaku yang homogen dengan bentuk geometris yang berbeda[4].
Lingkaran atau selongsong silinder tipis

Silinder berongga

Bidang segiempat

Silinder padat atau Cakram

METODOLOGI PENELITIAN
Alat dan materi yang diharapkan ialah seperangkat alat momen inersia OGAWASEIKI. Kemudian materi lainnya ialah lempengan sebanyak 3 buah dengan diameter yang berbeda. Mistar untuk mengukur diameter lempengan, neraca untuk menimbang lempengan dan juga beban serta katrol untuk daerah mengurangi goresan yang terjadi antara lempengan dan tali yang dihubungkan dengan beban. Selain itu, dibutuhkan kertas pita sebagai lintasan yang membuktikan percepatan sudut , beban untuk pemberat dan tali beban untuk penghubung antara beban dan lempengan.

Penyusunan alat di mulai dengan meletakkan lempengan besar di atas alat momen inersia ogawa seiki lalu di lilitkan pita pada lempengan besar dan benang yang di hubungkan pada katrol untuk di beri beban 0,05 kg. Setelah diberi beban maka beban dilepaskan dan diamati jarak lintasan pada pita. Kemudian diulangi dengan variasi beban 0,07 kg dan 0,09 kg. Dalam memilih Inew juga dilakukan dengan langkah yang sama, bedanya dengan meletakkan lempengan sedang diatas lemepengan besar lalu langkah prcobaanya sama dengan variasi beban. Setelah itu diganti lempengan sedang dengan lempengan kecil.

Data yang diperoleh berupa jarak (S) dan waktu (t) yang akan dihitung percepatannya. Cara mendapatkan besar dari percepatan yaitu dengan membuat grafik hubungan jarak (S) terhadap waktu (t) kuadrat dengan variasi beban pada setiap variasi lempeng. Dimana S merupakan variable terikat dan t²sebagai variable bebasnya, dan gradien dari grafik merupakan ½ percepatan. Persamaan itu didapatkan dari persamaan:S(t)= ½ at²

Hubungan antara momen gaya dengan percepatan sudut dapat diuraikan menjadi hubungan antara massa dengan percepatan linier. Grafik yang terbentuk merupakan grafik 1/a terhadap 1/m. grafik tersebut bertujuan untuk mencari momen inersia dari lempengan (silinder pejal) berukuran kecil, sedang, dan juga besar.

Gradien dari grafik tersebut masih berupa suatu rumusan lagi yaitu PEMBAHASAN Prinsip dari percobaan ini adalah suatu benda yang mengalami gerak rotasi atau melingkar terhadap suatu kerangka acuan tertentu akan mempunyai momen inersia. Momen inersia bergantung pada jenis dan bentuk bendanya.

Karena adanya gerak melingkar maka disana terdapat suatu kecepatan sudut ( ). Kecepatan sudut tersebut di hitung persatuan waktu sehingga di dapat percepatan sudut ( . Besar percepatan sudut itu sendiri dipengaruhi oleh berat dari massa benda yang di kaitkan. Semakin besar beban, maka dalam waktu yang sama, titik yang di hasilkan menjadi lebih panjang jaraknya, hal ini menunjukkan bahwa semakin besar percepatannya yang merupakan pengaruh dari gaya kebawah yang semakin besar.

Dari gerak rotasi yang dilakukan mengakibatkan adanya kecepatan sudut, momen inersia serta momen gaya. Saat terjadi gerak rotasi , kecepatan linear setiap bagian benda berbeda-beda pada pusat sumbu terjadi gerak yang lebih pelan di bandingkan dengan gerak yang ada di tepi yang cenderung lebih cepat. Besarnya percepatan yang terjadi dapat diketahui dari jarak titik yang ada pada kertas pita. Jarak 1 titik dengan titik lain adalah jarak yang di tempuh selama selang waktu 0,02 sekon. Dengan adanya pengaruh dari beban, mengakibatkan adanya percepatan, semakin besar massa beban maka semakin renggang jarak titik nya.Pada praktikum dilakukan 3 kali percobaan , dimana ketiganya menggunakan lempengan yang berbeda. Lempengan besar berjari-jari 0,15 m dan massa 1,04 kg.

Lempengan sedang 0,075 m dan massa 0,074 kg serta lempengan kecil dengan massa 0,024 kg dan jari jari 0,035 m. Dari masing-masing percobaan di dapat hasil yang sama, yaitu besarnya percepatan yang di tandai oleh titik, serta selang waktu tempuhnya. Besarnya percepatan dapat di hitung dengan metode grafik yaitu hubungan antara jarak (s) dengan kuadrat waktu tempuh (t²). S= V₀t + at²V_o dianggap 0 , karena kecepatan mula mula lempengan sebelum di ukur adalah 0 m , sehingga persamaannya menjadi S= at²Dibuat menjadi persamaan linear , s sebagai variabel terikat oleh t² sebagai variabel bebas. Sehingga akan di dapat kemiringan yang nilainya sama dengan a. Seperti yang ditunjukkan pada grafik seperti pada gambar berikut:

Gambar 1 grafik hubungan S(m) terhadap t² (s²) pada lempengan besarDari hubungan tersebut diketahui bahwa a=2m. Dari grafik di dapat nilai a pada lempeng besar untuk beban 0,05 kg sebesar 0,824 m/s² untuk beban 0,07 kg sebesar 0,986 m/ s² dan untuk beban 0,09 kg sebesar 01,070 m/s² pada lempeng kecil untuk beban 0,05 kg sebesar 0,356 m/s² untuk beban 0,07 kg sebesar 0,354 m/s² dan untuk beban 0,09 kg sebesar 0,490 m/s².

Pada lempeng sedang untuk beban 0,05 kg sebesar 0,548 m/s² untuk beban 0,07 kg sebesar 0,644 m/s² dan untuk beban 0,09 kg sebesar 0,736 m/s².Setelah di dapatkan nilai a, dimasukkan ke persamaan kedua yang telah di turunkan di depan . Persamaan ini dapat di gunakan untuk mencari besarnya nilai momen inersia (I) . 1/a = 1/a sebagai variable terikat yang besarnya bergantung pada 1/m yang merupakan variable bebasnya. Perpotongan di sumbu y senilai dengan 1/g serta kemiringannya m . Sehingga nilai I m.Ra.Rb.g dan g 1/c.
Penerapan Momen Inersia

Hasil data yang diperoleh dapat di buat grafik hubungan antara 1/a terhadap 1/m seperti di bawah ini:

Grafik hubungan 1/a (s²/m) terhadap 1/m (kg^-1)Selain menggunakan metode grafik, perhitungan momen inersia juga dilakukan secara manual, dengan menggunakan percepatan gravitasi 9,8 m/s². Hasil dari perhitungan grafik dan manual sangatlah berbeda. Nilai gravitasi dari grafik didapatkan pada persamaan pertama untuk I_o sebesar 1,745 m/s² untuk I_sedang sebesar 1,259 m/ s² dan untuk I_kecil sebesar 0,709 m/s². Nilai gravitasi pada grafik masing- masing percobaan berbeda dan sangat jauh dari literatur. Hal tersebut disebabkan berbagai faktor diantaranya karena dalam perhitungan grafik semua komponen diperhitungkan seperti massa dan jari-jari termasuk presentase kesalahan relatif di hitung sedangkan pada perhitungan manual hanya dihitung sesuai rumus dan ketelitiannya juga tidak terlalu besar.

Selain di tentukan momen inersia dari masing masing lempengan, di cari pula besar nilai I₀ yang merupakan besar momen inersia dari lempengan besar. Kemudian dicari I_new yang merupakan penggabungan nilai momen inersia. I_new = I₀ I_new = I₀ + I₂ + …Semakin besar massa dan jari-jari silinder , maka nilai momen inersia menjadi semakin besar .Hal ini dapat dilihat dari persamaan I₀ = MR² , dimana hubungan antara massa dan momen inersia menunjukkan kesebandingan. Pada percobaan yang telah dilakukan , terdapat beberapa ketidakakuratan, yang di sebabkan oleh system maupun praktikan itu sendiri . Kesalahan system seperti Gerak rotasi yang tidak sempurna akibat pengaruh getaran maupun yang lainnya .

Serta seringkali terdapat kesalahan praktikan yang kurang akurat dalam membaca jarak antar titik – titik percepatannya.KESIMPULANBerdasarkan praktikum yang telah dilakukan dapat disimpulkan bahwa :1. Hubungan antara momen gaya dengan percepatan sudut dalam gerak melingkar dengan :Besarnya momen gaya sebanding dengan percepatan sudut , dimana besarnya dipengaruhi oleh jarak dan waktu tempuh.2. Besarnya nilai momen inersia dengan menggunakan metode grafik dan manual

1/a (s²/m)

Sehingga I = m.Ra.Rb.g

dengan g : 1/c

1/m (1/kg)

Sedangkan secara matematis : I = m.Ra.Rb.g dengan g =9,8 m/s²hasil yang diperoleh sangatlah berbeda

Pada percobaan ini akan dibahas perihal momen inersia suatu benda tegar dengan cara menguji kekerabatan antara momen gaya dengan percepatan sudut. Metode percobaan ini dengan melaksanakan percobaan sebanyak 3 kali dengan memakai variasi dari lempengan dan variasi massa beban yang digantungkan pada katrol. pada percobaan tersebut diketahui kekerabatan antara momen gaya dan percepatan sudut. Dimana momen gaya mempunyai kekerabatan kesebandingan dengan percepatan sudutnya sehingga semakin besar percepatan sudutnya maka momen gayanya akan semakin besar dan sebaliknya. Dimana momen gaya merupakan hasil kali antara momen inersia dan percepatan sudut yang dilakukan benda tegar.

Dari hasil pengolahan data mampu diperoleh momen inersia pada tiga buah lempengan dengan jari-jari yang berbeda. diperoleh momen inersia dengan metode perhitungan matematis sebesar 2,39 x10-2 kgm2; 2,36 x 10-2 kgm2dan 2,341 x10-2 kgm2 ,dengan memakai percepatan gravitasi pada literatur yaitu 9,8 m/s2 diperoleh momen inersia sebesar 7,01 x10-3 kgm2; 5,72 x10-3 kgm2; dan 3,9×10-3 kgm2; dan dengan grafik diperoleh momen inersia sebesar 12,5 x 10-4kgm2 ; 7,35 x 10-4 kgm2; dan 2,82 x10-4 kgm2.
Rumus Momen Inersia

PENDAHULUAN
Setiap benda mempunyai kecenderungan untuk mempertahankan keadaan geraknya. Jika dalam keadaan membisu benda cenderung untuk tetap diam. Demikian pula jikalau benda sedang bergerak lurus beraturan, benda cenderung tetap bergerak lurus beraturan. Kecenderungan ini disebut inersia dan ukuran kecenderungan ini dinamakan massa.
Konsep tersebut juga berlaku pada benda yang sedang berotasi, mirip halnya planet-planet di dalam tata surya mempunyai kecenderungan untuk tetap mempertahankan keadaan gerak rotasinya. Kecenderungan ini disebut momen inersia atau rotasi inersia. Hal ini mampu ditemukan dalam kehidupan sehari-hari.

Roda-roda sepeda yang berputar bergotong-royong turut membantu pengendara biar sepeda tetap berdiri. Hal ini dikarenakan roda-roda sepeda itu cenderung tetap berputar pada bidang yang sama sehingga menciptakan sepeda lebih gampang untuk dikendarai.
Telah diketahui bahwa massa benda hanya bergantung pada jumlah kandungan zat di dalam benda.

Perbedaannya dengan momen inersia yang selain bergantung pada kandungan zat di dalamnya atau massa benda, juga bergantung pada posisi massa tersebut ke sumbu putarnya. Semakin jauh posisi massa benda ke sentra rotasinya, semakin besar momen inersia benda tersebut.

Untuk lebih memahami perihal momen inersia maka dilakukanlah praktikum kali ini yang bertujuan untuk mengetahui kekerabatan antara momen gaya dan percepatan sudut pada gerak melingkar, memilih besarnya nilai momen inersia dan membandingkannya dengan nilai yang terprediksi, serta mengetahui kekerabatan Inew (momen inersia benda terbebani) dengan I0 (momen inersia mula-mula).

TINJAUAN PUSTAKA
Momen inersia merupakan sifat kelembaman suatu benda yang berotasi atau dirotasikan terhadap sumbu tertentu. Momen inersia dinyatakan dengan simbol I, merupakan suatu besaran yang memperlihatkan perjuangan dari suatu sistem benda untuk menentang gerak rotasinya. Momen inersia juga memberikan kecenderungan suatu sistem benda untuk terus berputar atau membisu sebagai reaksi terhadap gaya torsi dari luar. Jika suatu benda yang bebas berputar terhadap sebuah sumbu sulit untuk dibentuk berputar, maka momen inersianya terhadap sumbu itu besar [1]

Ketika sudut benda tegar mengalami percepatan, berarti benda tersebut mempunyai percepatan sudut. Jika ω1 dan ω2 merupakan kecepatan sudut pada waktu t1 dan t2, percepatan sudut rata-rata α11 mampu dihitung:
(1)
Percepatan sudut sesaat α yakni limit α11 pada dikala ∆t mendekati 0
(definisi percepatan sudut) (2)
Satuan percepatan sudut α yakni rad/sekon.[2]
Didefinisikan bahwa besarnya torsi yang terkait oleh gaya F oleh persamaan
(3)
dimana r merupakan jarak antara titik sentra dan titik yang diberi F, serta d yakni jarak tegak lurus dari titik sentra ke garis arah F. Besaran d disebut lengan momen (lengan pengungkit) dari F[5].
Gaya tangensial menghasilkan percepatan tangensial at dan
(4)
Besar torsi terhadap sentra bulat yang diakibatkan oleh gaya Ft adalah
(5)
Karena percepatan tangensial berafiliasi dengan percepatan sudut dengan persamaan sehingga besarnya torsi menjadi

(6)

Artinya torsi yang bekerja pada partikel sebanding dengan percepatan sudutnya[2].
yakni momen inersia partikel bermassa m, yang berotasi sejauh r dari sumbu rotasi. persamaan ini juga menyatakan kekerabatan antara torsi, momen inersia dan percepatan sudut partikel yang melaksanakan gerak rotasi. Istilah kerennya, ini yakni persamaan Hukum II Newton untuk partikel yang berotasi.
Dari aturan II Newton kita ketahui bahwa: (7)
Torsi berafiliasi dengan gaya yang bekerja terhadap sentra dan dinyatakan dengan

(8)

                                                                              (9)[3].

Momen inersia pada benda kaku yang homogen dengan bentuk geometris yang berbeda[4].
Lingkaran atau selongsong silinder tipis

Silinder berongga

Bidang segiempat

Silinder padat atau Cakram

METODOLOGI PENELITIAN
Alat dan materi yang dibutuhkan yakni seperangkat alat momen inersia OGAWASEIKI. Kemudian materi lainnya yakni lempengan sebanyak 3 buah dengan diameter yang berbeda. Mistar untuk mengukur diameter lempengan, neraca untuk menimbang lempengan dan juga beban serta katrol untuk kawasan mengurangi tabrakan yang terjadi antara lempengan dan tali yang dihubungkan dengan beban.

Selain itu, dibutuhkan kertas pita sebagai lintasan yang menandakan percepatan sudut , beban untuk pemberat dan tali beban untuk penghubung antara beban dan lempengan.
Penyusunan alat di mulai dengan meletakkan lempengan besar di atas alat momen inersia ogawa seiki kemudian di lilitkan pita pada lempengan besar dan benang yang di hubungkan pada katrol untuk di beri beban 0,05 kg.

Setelah diberi beban maka beban dilepaskan dan diamati jarak lintasan pada pita. Kemudian diulangi dengan variasi beban 0,07 kg dan 0,09 kg. Dalam memilih Inew juga dilakukan dengan langkah yang sama, bedanya dengan meletakkan lempengan sedang diatas lemepengan besar kemudian langkah prcobaanya sama dengan variasi beban. Setelah itu diganti lempengan sedang dengan lempengan kecil.

Data yang diperoleh berupa jarak (S) dan waktu (t) yang akan dihitung percepatannya. Cara menerima besar dari percepatan yaitu dengan menciptakan grafik kekerabatan jarak (S) terhadap waktu (t) kuadrat dengan variasi beban pada setiap variasi lempeng. Dimana S merupakan variable terikat dan t2 sebagai variable bebasnya, dan gradien dari grafik merupakan ½ percepatan. Persamaan itu didapatkan dari persamaan:
S(t)= ½ at2
Hubungan antara momen gaya dengan percepatan sudut mampu diuraikan menjadi kekerabatan antara massa dengan percepatan linier. Grafik yang terbentuk merupakan grafik 1/a terhadap 1/m. grafik tersebut bertujuan untuk mencari momen inersia dari lempengan (silinder pejal) berukuran kecil, sedang, dan juga besar. Gradien dari grafik tersebut masih berupa suatu rumusan lagi yaitu
PEMBAHASAN
Prinsip dari percobaan ini yakni suatu benda yang mengalami gerak rotasi atau melingkar terhadap suatu kerangka contoh tertentu akan mempunyai momen inersia. Momen inersia bergantung pada jenis dan bentuk bendanya. Karena adanya gerak melingkar maka disana terdapat suatu kecepatan sudut ( ). Kecepatan sudut tersebut di hitung persatuan waktu sehingga di mampu percepatan sudut ( . Besar percepatan sudut itu sendiri dipengaruhi oleh berat dari massa benda yang di kaitkan. Semakin besar beban, maka dalam waktu yang sama, titik yang di hasilkan menjadi lebih panjang jaraknya, hal ini memberikan bahwa semakin besar percepatannya yang merupakan efek dari gaya kebawah yang semakin besar.

Dari gerak rotasi yang dilakukan menimbulkan adanya kecepatan sudut, momen inersia serta momen gaya. Saat terjadi gerak rotasi , kecepatan linear setiap penggalan benda berbeda-beda pada sentra sumbu terjadi gerak yang lebih pelan di bandingkan dengan gerak yang ada di tepi yang cenderung lebih cepat. Besarnya percepatan yang terjadi mampu diketahui dari jarak titik yang ada pada kertas pita. Jarak 1 titik dengan titik lain yakni jarak yang di tempuh selama selang waktu 0,02 sekon. Dengan adanya efek dari beban, menimbulkan adanya percepatan, semakin besar massa beban maka semakin renggang jarak titik nya.

Pada praktikum dilakukan 3 kali percobaan , dimana ketiganya memakai lempengan yang berbeda. Lempengan besar berjari-jari 0,15 m dan massa 1,04 kg. lempengan sedang 0,075 m dan massa 0,074 kg serta lempengan kecil dengan massa 0,024 kg dan jari jari 0,035 m. Dari masing-masing percobaan di mampu hasil yang sama, yaitu besarnya percepatan yang di tandai oleh titik, serta selang waktu tempuhnya. Besarnya percepatan mampu di hitung dengan metode grafik yaitu kekerabatan antara jarak (s) dengan kuadrat waktu tempuh (t2).
S= V0t + at2
Vo dianggap 0 , lantaran kecepatan mula mula lempengan sebelum di ukur yakni 0 m , sehingga persamaannya menjadi
S= at2
Dibuat menjadi persamaan linear , s sebagai variabel terikat oleh t2 sebagai variabel bebas. Sehingga akan di mampu kemiringan yang nilainya sama dengan a. Seperti yang ditunjukkan pada grafik mirip pada keterangan berikut:
Grafik kekerabatan S(m) terhadap t2 (s2) pada lempengan besar

grafik kekerabatan S(m) terhadap t2 (s2) pada lempengan besar
Dari kekerabatan tersebut diketahui bahwa a=2m. Dari grafik di mampu nilai a pada lempeng besar untuk beban 0,05 kg sebesar 0,824 m/s2 untuk beban 0,07 kg sebesar 0,986 m/ s2 dan untuk beban 0,09 kg sebesar 01,070 m/s2 pada lempeng kecil untuk beban 0,05 kg sebesar 0,356 m/s2 untuk beban 0,07 kg sebesar 0,354 m/s2 dan untuk beban 0,09 kg sebesar 0,490 m/s2. Pada lempeng sedang untuk beban 0,05 kg sebesar 0,548 m/s2 untuk beban 0,07 kg sebesar 0,644 m/s2 dan untuk beban 0,09 kg sebesar 0,736 m/s2.

Setelah di dapatkan nilai a, dimasukkan ke persamaan kedua yang telah di turunkan di depan . Persamaan ini mampu di gunakan untuk mencari besarnya nilai momen inersia (I) .
1/a =
1/a sebagai variable terikat yang besarnya bergantung pada 1/m yang merupakan variable bebasnya. Perpotongan di sumbu y senilai dengan 1/g serta kemiringannya m . Sehingga nilai I m.Ra.Rb.g dan g 1/c. Hasil data yang diperoleh mampu di buat grafik kekerabatan antara 1/a terhadap 1/m mirip di bawah ini:
Grafik kekerabatan 1/a (s2/m) terhadap 1/m (kg-1)
Faktor Momen Inersia

Rumus, Contoh Soal, Penerapan, Faktor Dan Pengertian Momen Inersia

Gambar 2. Grafik kekerabatan 1/a (s2/m) terhadap 1/m (kg-1)
Selain memakai metode grafik, perhitungan momen inersia juga dilakukan secara manual, dengan memakai percepatan gravitasi 9,8 m/s2. Hasil dari perhitungan grafik dan manual sangatlah berbeda. Nilai gravitasi dari grafik didapatkan pada persamaan pertama untuk Io sebesar 1,745 m/s2 untuk Isedang sebesar 1,259 m/ s2 dan untuk Ikecil sebesar 0,709 m/s2. Nilai gravitasi pada grafik masing- masing percobaan berbeda dan sangat jauh dari literatur.

Hal tersebut disebabkan aneka macam faktor diantaranya lantaran dalam perhitungan grafik semua komponen diperhitungkan mirip massa dan jari-jari termasuk presentase kesalahan relatif di hitung sedangkan pada perhitungan manual hanya dihitung sesuai rumus dan ketelitiannya juga tidak terlalu besar.

Selain di tentukan momen inersia dari masing masing lempengan, di cari pula besar nilai I0 yang merupakan besar momen inersia dari lempengan besar. Kemudian dicari Inew yang merupakan penggabungan nilai momen inersia.
Inew = I0
Inew = I0 + I2 + …
Semakin besar massa dan jari-jari silinder , maka nilai momen inersia menjadi semakin besar .Hal ini mampu dilihat dari persamaan I0 = MR2 , dimana kekerabatan antara massa dan momen inersia memberikan kesebandingan.

Pengertian Momen Inersia : Faktor, Penerapan, Contoh Soal Dan Rumusnya

Rumus, Contoh Soal, Penerapan, Faktor Dan Pengertian Momen Inersia

Pengertian Nemathelminthes : Contoh, Manfaat, Peranan, Ciri, Siklus Hidup

Pengertian Saham Dan Obligasi : Preven, Dividen Dan Contohnya

Fungsi Organ Mulut Menurut Para Ahli